I’ve been encouraged to apply the type of analysis from my previous post to another situation.
I’ll follow the same format. (Did I mention that I’m lazy?)
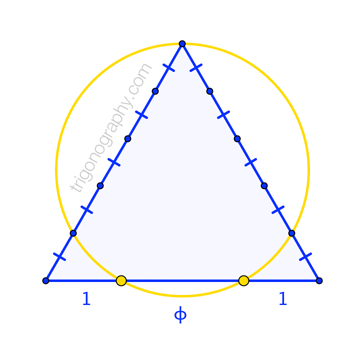
The figure shows one of Đào Thanh Oai’s constructions of the golden ratio, \(\phi = 1.618\dots\).
Paraphrasing …
The circle through a vertex of an equilateral triangle, and through points one-fifth of the way up the adjacent sides, separates the third side into segments whose lengths are in the proportion $$1 \;:\; \phi \;:\; 1$$
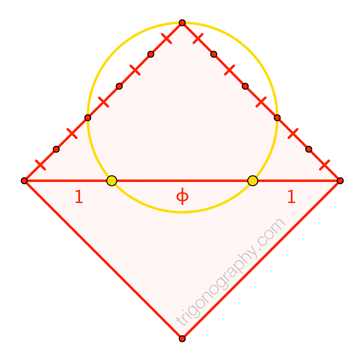


For the general analysis, we consider an isosceles triangle with legs of unit length and vertex angle of half-measure \(\theta\). And we suppose that the circle through the vertex, and through points at distance \(s\) up the legs, separates the base in proportion \(1:r:1\) (for not-necessarily-golden ratio \(r\)), as shown. Calculating the power of a base vertex with respect to the circle in two ways (along the leg, along the base) gives …
$$s \cdot 1 = 2 x \cdot (2 x + 2 x r ) = 4 x^2 (1 + r)$$
Then, since \(\sin\theta = 2 x + x r = x (2 +r)\),
we can write …
$$s = 4 \sin^2\theta\;\frac{1+r}{(2+r)^2} \qquad(\star)$$
In the particular case \(r = \phi\), the fraction in \((\star)\) doesn’t completely vanish as it did before;
it reduces to \(1/5\):
\displaystyle \qquad\quad s = \frac{4}{5}\sin^2\theta\qquad\text{or}\qquad \sin\theta = \frac{\sqrt{s}}{2}\cdot\frac{\sqrt{5}}{5}
\end{array}$$
\theta &= \;\;0^\circ :\; s = 0/5 \\[4pt]
\theta &= \color{blue}{30^\circ} :\; s = \color{blue}{1}/5 \quad\to\quad\text{Đào’s Triangle}\\[4pt]
\theta &= \color{red}{45^\circ} :\; s = \color{red}{2}/5 \quad\to\quad\text{Đào’s Square}\\[4pt]
\theta &= \color{violet}{60^\circ} :\; s = \color{violet}{3}/5 \quad\to\quad\text{Someone’s Hexagon}\\[4pt]
\theta &= 90^\circ :\; s = 4/5
\end{align}$$
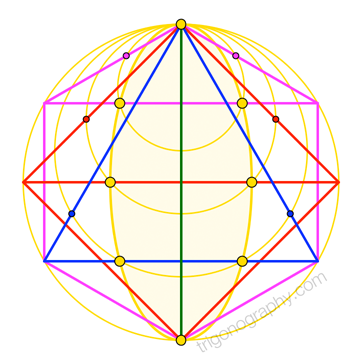
Along with the degenerate cases for \(0^\circ\) and \(90^\circ\), the triangle, square, and hexagon configurations exhaust all possibilities of Đào-like constructions involving an “\(n\)-fifths circle” for integer \(n\).
The diagram at right combines the corresponding figures within a common circumcircle, and with a companion ellipse through separation points on appropriate chords. In this context, the chord for the \(90^\circ\) figure collapses to a point, which actually obscures an important phenomenon.
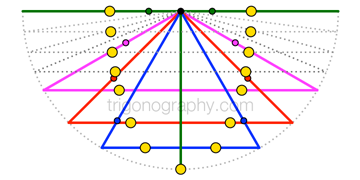
Holding the edges to a constant length (and focusing on the isosceles triangles formed with the chords), we find that the \(90^\circ\) case, in and of itself, is problematic: the corresponding “four-fifths circle” is actually a straight line that coincides with the flat triangle’s legs and its base, making the locations of the separation points undefined. The problem resolves, however, when this case is viewed as the limiting form in the continuous family of triangles. (An analogous observation can/should be added to my previous article. (Lazy!) )