$$\left.\begin{align}
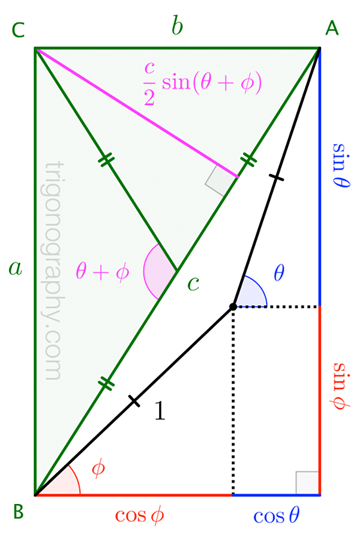
\sin\theta + \sin\phi &= a \\[4pt]
\cos\theta + \cos\phi &= b
\end{align}\quad\right\} \quad\Longrightarrow\quad\sin\left(\theta+\phi\right) = \frac{2ab}{a^2+b^2}$$
\sin\theta + \sin\phi &= a \\[4pt]
\cos\theta + \cos\phi &= b
\end{align}\quad\right\} \quad\Longrightarrow\quad\sin\left(\theta+\phi\right) = \frac{2ab}{a^2+b^2}$$
$$a b \;=\; 2|\triangle ABC| \;=\; c \cdot \frac{c}{2}\sin\left(\alpha+\beta\right)
\quad\Longrightarrow\quad\sin\left(\alpha + \beta\right) = \frac{2ab}{c^2}$$
Motivated by this question on the Mathematics Stack Exchange.