2\,\sinh u &\;=\; e^{u} -\, e^{-u} \\[4pt]
2\,\cosh u &\;=\; e^{u} + e^{-u}
\end{align}$$
$$\begin{align}
|\overline{OX}|\cdot|\overline{XY}| \;\equiv\; 1 &\quad\to\quad u = \int_{1}^{|\overline{OX}|} \frac{1}{t}dt \;=\; \ln |\overline{OX}| \\[6pt]
&\quad\to\quad |\overline{OX}| = e^{u} \quad\text{and}\quad |\overline{XY}| = e^{-u}
\end{align}$$
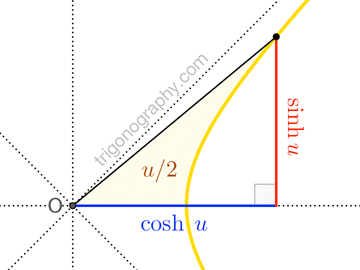
Some background. Geometrically, we define \(\sinh u\) and \(\cosh u\) by direct analogy with \(\sin\theta\) and \(\cos\theta\): as certain perpendicular segments associated with an arc of the “unit hyperbola”, \(x^2 – y^2 = 1\).
While \(\theta\) is usually interpreted as the length of a circular arc, we note that it is also twice the area of the corresponding circular sector. The hyperbolic parameter \(u\) is interpreted via area, as well; today’s trigonograph shows why:
Conveniently scaling lengths in the unit hyperbola figure by \(\sqrt{2}\) —and, thus, scaling areas by \(2\)—
we see that \(\sinh u\) and \(\cosh u\) are directly computable from \(u\) via the exponential function!
(In fact, we can say the same of \(\sin\theta\) and \(\cos\theta\), but we need complex exponentials for that.)
Taken from this answer of mine on the Mathematics Stack Exchange.
