Attributed to mathematician and teacher Y. S. Chaikovsky, circa 1935.
(Gurin, Leo S. ”A Problem.” The American Mathematical Monthly 103, no. 8 (1996): 683-86. JSTOR)
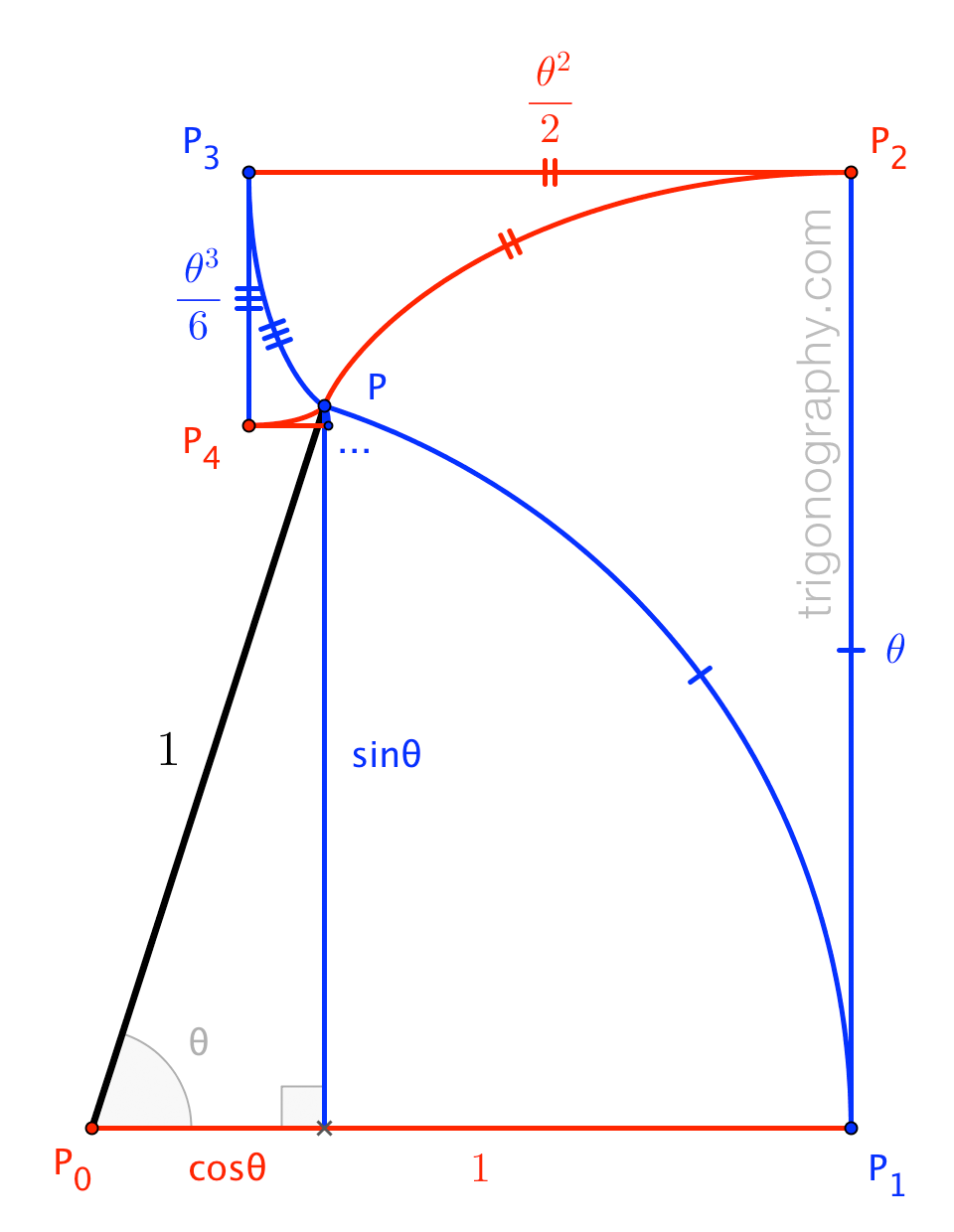
\(\stackrel{\frown}{PP}_1\) is an arc of the unit circle; thereafter, \(\stackrel{\frown}{PP}_i\) is an involute of \(\stackrel{\frown}{PP}_{i-1}\).
$$
\begin{align}
\cos\theta &\;=\; |\overline{P_0P_1}| \;-\; |\overline{P_2 P_3}| \;+\; |\overline{P_4P_5}| \;-\; \cdots \\[4pt]
&\;=\; |\overline{P_0P}| \;-\; |\stackrel{\frown}{P_2 P}| \;+\; |\stackrel{\frown}{P_4P}| \;-\; \cdots \\[4pt]
&\;=\; \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k)!}\;\theta^{2k} \\[12pt]
\sin\theta &\;=\; |\overline{P_1P_2}| \;-\; |\overline{P_3 P_4}| \;+\; |\overline{P_5P_6}| \;-\; \cdots \\[4pt]
&\;=\; |\overline{P_1P}| \;-\; |\stackrel{\frown}{P_3 P}| \;+\; |\stackrel{\frown}{P_5P}| \;-\; \cdots \\[4pt]
&\;=\; \sum_{k=0}^{\infty} \frac{(-1)^k}{(2k+1)!}\;\theta^{2k+1}
\end{align}$$
\begin{align}
\cos\theta &\;=\; |\overline{P_0P_1}| \;-\; |\overline{P_2 P_3}| \;+\; |\overline{P_4P_5}| \;-\; \cdots \\[4pt]
&\;=\; |\overline{P_0P}| \;-\; |\stackrel{\frown}{P_2 P}| \;+\; |\stackrel{\frown}{P_4P}| \;-\; \cdots \\[4pt]
&\;=\; \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k)!}\;\theta^{2k} \\[12pt]
\sin\theta &\;=\; |\overline{P_1P_2}| \;-\; |\overline{P_3 P_4}| \;+\; |\overline{P_5P_6}| \;-\; \cdots \\[4pt]
&\;=\; |\overline{P_1P}| \;-\; |\stackrel{\frown}{P_3 P}| \;+\; |\stackrel{\frown}{P_5P}| \;-\; \cdots \\[4pt]
&\;=\; \sum_{k=0}^{\infty} \frac{(-1)^k}{(2k+1)!}\;\theta^{2k+1}
\end{align}$$
While the trigonograph makes the convergence of the series clear, the fact that
the involute lengths are appropriately-scaled powers of \(\theta\) is decidedly not.
Gurin’s article explains Chaikovsky’s clever use of of combinatorics
(and a fundamental limit from Calculus) to prove the connection, but
one may also treat this as an exercise in parametric arc length and recursion.
Get the t-shirt … or the other one!
