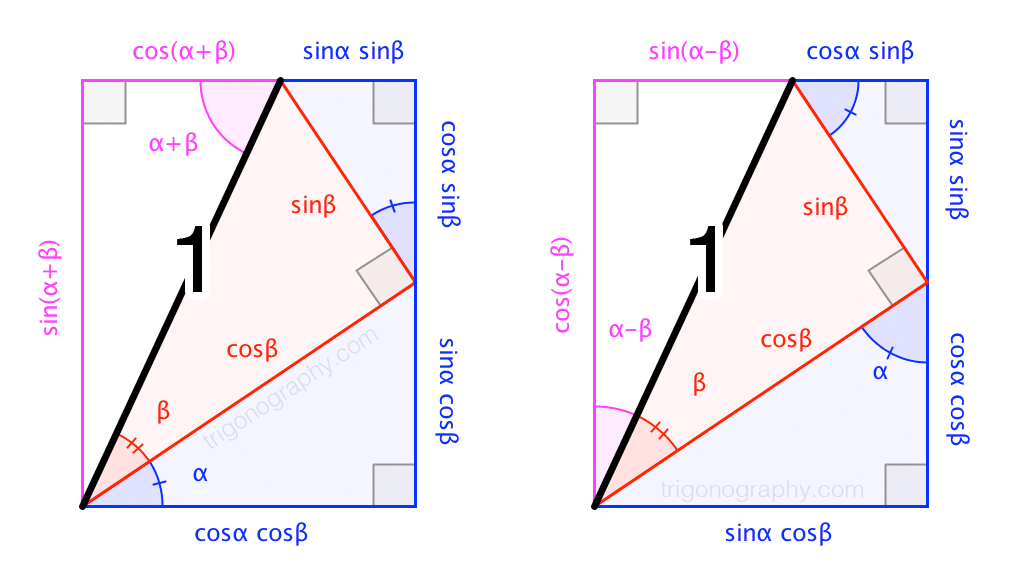
For \(\alpha\), \(\beta\), \(\alpha\pm\beta\) between \(0^\circ\) and \(90^\circ\):
$$\begin{align}
\sin(\alpha \pm \beta ) &= \sin\alpha \cos\beta \pm \cos\alpha \sin\beta \\[4pt]
\cos(\alpha \pm \beta ) &= \cos\alpha \cos\beta \mp \sin\alpha \sin\beta\end{align}$$
\sin(\alpha \pm \beta ) &= \sin\alpha \cos\beta \pm \cos\alpha \sin\beta \\[4pt]
\cos(\alpha \pm \beta ) &= \cos\alpha \cos\beta \mp \sin\alpha \sin\beta\end{align}$$
Adapting the trigonographs for angles outside the given range
makes for a nice exercise.
Fun Fact: Wikipedia’s “List of Trigonometric Identities” entry
features the trigonograph on the left. (I’m famous-ish!)
