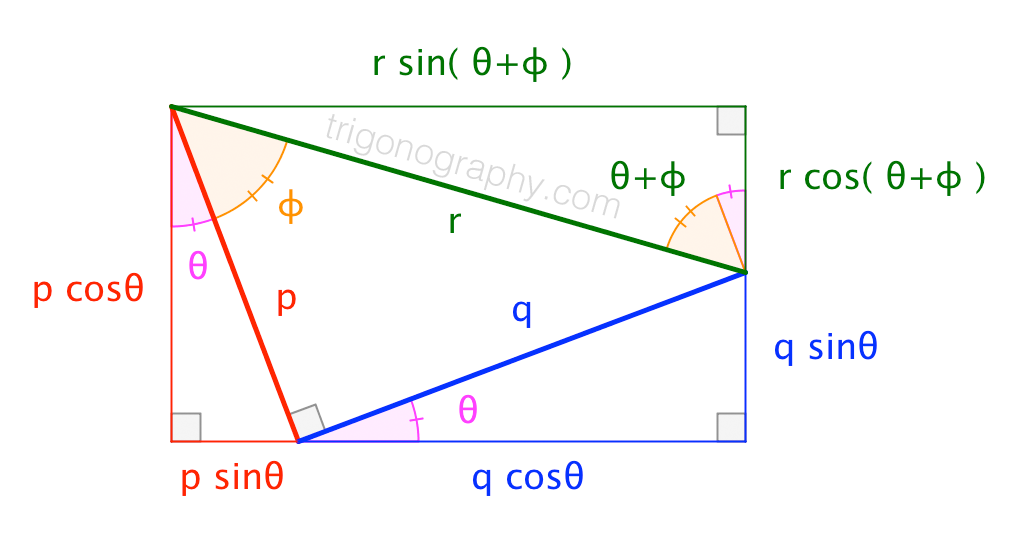
For \(\theta\) between \(0^\circ\) and \(90^\circ\):
$$\begin{align}
p \sin\theta \,+\, q\cos\theta &\;=\; r \sin(\,\theta+\phi\,) \\
p \cos\theta \,-\, q\sin\theta &\;=\; r \cos(\,\theta+\phi\,) \\[6pt]
\text{where}\quad p^2 + q^2 = r^2 &\quad\text{and}\quad \tan\phi = q/p
\end{align}$$
p \sin\theta \,+\, q\cos\theta &\;=\; r \sin(\,\theta+\phi\,) \\
p \cos\theta \,-\, q\sin\theta &\;=\; r \cos(\,\theta+\phi\,) \\[6pt]
\text{where}\quad p^2 + q^2 = r^2 &\quad\text{and}\quad \tan\phi = q/p
\end{align}$$
The resemblance to these trigonographs is no coincidence. (Why?)