$$\begin{align}
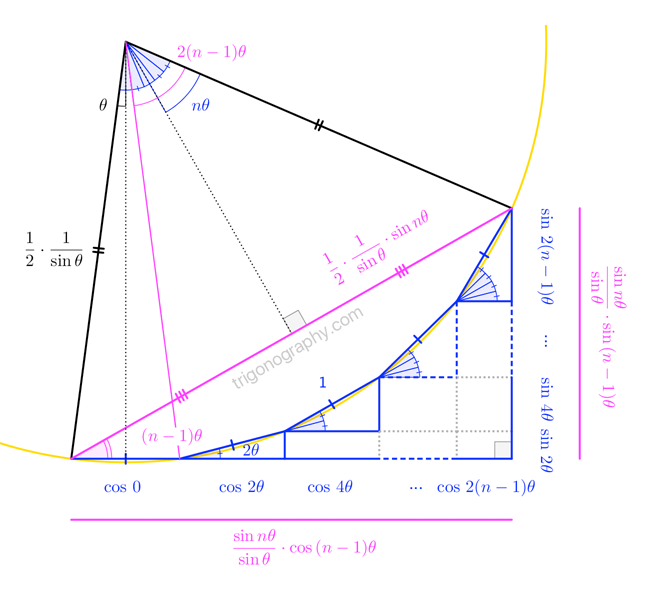
\sum_{k=0}^{n-1}\;\sin\,2k\theta \;=\; \frac{\sin\,n\theta}{\sin\theta}\cdot\sin\,(n-1)\theta \\[8pt]
\sum_{k=0}^{n-1}\;\cos\,2k\theta \;=\; \frac{\sin\,n\theta}{\sin\theta}\cdot\cos\,(n-1)\theta
\end{align}$$
\sum_{k=0}^{n-1}\;\sin\,2k\theta \;=\; \frac{\sin\,n\theta}{\sin\theta}\cdot\sin\,(n-1)\theta \\[8pt]
\sum_{k=0}^{n-1}\;\cos\,2k\theta \;=\; \frac{\sin\,n\theta}{\sin\theta}\cdot\cos\,(n-1)\theta
\end{align}$$