This is George Odom‘s elegant construction of the ever-fascinating golden ratio, \(\phi\):
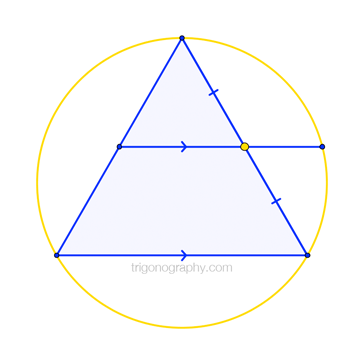
If \(a\) measures a “midpoint segment” of an equilateral triangle, and if \(b\) measures the extension of that segment meeting the triangle’s circumcircle, then $$\frac{a}{b} = \phi = 1.618\dots$$
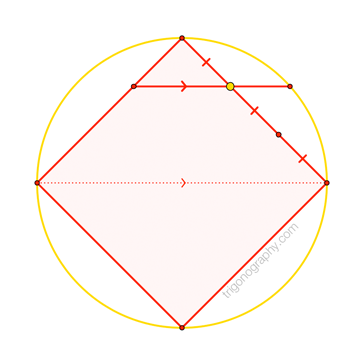
It’s possible —even likely— that all of these observations already appear somewhere in
the vast lore on the golden ratio, but I’m too lazy to do a literature search.
published in 2015 by Q. H. Tran (PDF). Curiously, despite noting the Odom-esque flavor of his result,
Tran doesn’t seem to realize that his figure features an obvious, and even-more-Odom-esque,
segment trisector. (The missed connection with the square is less surprising, given the semi-circular
context.) Nevertheless, it appears appropriate to assign priority to what I’ll call “Tran’s Square”.
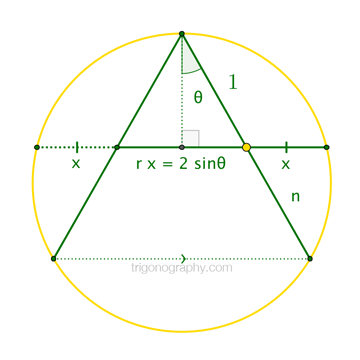
To see the underlying connections here, consider an inscribed angle of half-measure \(\theta\), and suppose the “\((n+1)\)-secting segment” through the sides of this angle is such that the ratio of its length to that of its circle-meeting extension is \(r : 1\), for some not-necessarily-golden ratio \(r\).
$$n\cdot 1 = x \cdot ( x + r x )\quad\to\quad x = \sqrt{\frac{n}{1+r}}$$
But, clearly, we also have \(r x = 2\sin\theta\), so that
$$\sin\theta = \frac{rx}{2} = \frac{\sqrt{n}}{2}\cdot\frac{r}{\sqrt{1+r}}\qquad(\star)$$
from the common mnemonic
involving trig’s “special angles” …
\sin \phantom{0}0^\circ &= \sqrt{0}\,/2 \\[4pt]
\sin \color{blue}{30^\circ} &= \sqrt{\color{blue}{1}}\,/2 \quad\to\quad\text{Odom’s Triangle}\\[4pt]
\sin \color{red}{45^\circ} &= \sqrt{\color{red}{2}}\,/2 \quad\to\quad\text{Tran’s Square}\\[4pt]
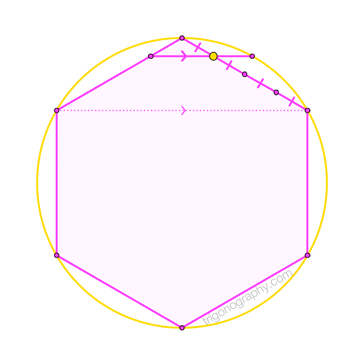
\sin \color{violet}{60^\circ} &= \sqrt{\color{violet}{3}}\,/2 \quad\to\quad\text{Someone’s Hexagon} \\[4pt]
\sin 90^\circ &= \sqrt{4}\,/2
\end{align}$$
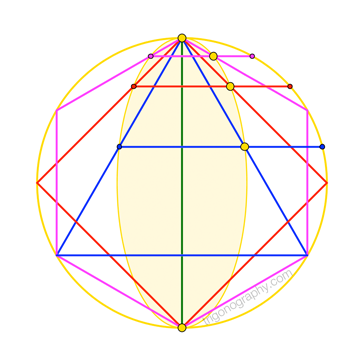
Our sine relation establishes that \(n\) cannot exceed four. Therefore, the triangle, square, and hexagon above represent all available (non-degenerate) Odom-like constructions for integer \(n\). The composite view at right shows a bonus feature: All the dividing points lie on an ellipse. (No, the ellipse isn’t “golden”: neither its eccentricity, nor its aspect ratio, is \(\phi\).)
Of course, no one requires \(n\) to be an integer,
so there remains more to say. For instance, the Odom-like construction for the regular pentagon, which already admits so many connections with the golden ratio, has \(n = \phi^2 = \phi+1\). Also, \(n = \phi\) implies \(\theta \approx 39.49^\circ \). (Is there anything (else) remarkable about that angle?) And so on.
I’ll leave further considerations to the reader.